| How Does an Eprom work?Simple as A B C D E F | 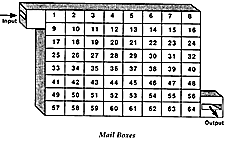
| Mail Boxes
The Eprom is a basic device which can be considered simply as a block of "mail boxes", each holding a message. Each "box" is numbered consecutively. At one end of the block of "boxes" is a slot and by posting the Address or ADDRESS of a particular "box" into this slot you will make its message contents appear from the output slot at the other end of the block.
You can read the contents of ANY "box" in this manner if you know its number. |
Messages in Code The actual message in each box consists of just eight numbers, each of which can be "1" or "0".
So a typical message might be 1 1 0 1 0 0 0 1
The number of each box can also be represented as a code.
For instance:-
the first box address may be 0 0 0 0 0 0 0 0 0 0 0 1
and the second box could be 0 0 0 0 0 0 0 0 0 0 1 0
In practice, the box ADDRESS is applied to the Eprom input pins as high or low voltages representing "1" or "0".
The CONTENTS of the selected box appear on the eight Eprom output pins as high or low voltages.
For instance the box with address:- A11 A10 A9 A8 A7 A6 A5 A4 A3 A2 A1 A0 input pins
0 0 0 0 0 0 1 0 1 0 1 0 might have the contents:- D7 D6 D5 D4 D3 D2 D1 D0 output pins
1 1 1 0 1 0 0 1 As the ADDRESS of each box is applied to the input pins, so the CONTENTS of that box appear as voltages on the 8 output pins.
Bits in Line
Eproms work quite happily with binary codes consisting only of "1"s and "0"s, called "bits". We use the designations "1" and "0" simply for convenience to represent high voltage and low voltage respectively. The actual voltages are usually not critical - high will be some positive voltage equal to, or slightly less than, the supply voltage. Low voltage will usually be less than 1 volt. The position of each "bit" in line represents its actual value:-
128 64 32 16 8 4 2 1
the code 1 0 1 1 0 0 1 0 adds up to 178 in decimal.
Horrible Hex
That was a little tedious to work out but it is difficult to use decimal with Eproms. To make the numbers easier to deal with we can use the system called Hexadecimal. Before you shriek in horror at this word let me advise you that everything you ever read about how difficult it is, is nonesense. It makes life very easy indeed.
"Hexadecimal uses the base sixteen". That means that you count up to 16, carry one, then start again. In fact we use letters to represent numbers bigger than 9, as follows:-
0 1 2 3 4 5 6 7 8 9 A B C D E F
F represents ordinary decimal 15 and is as high as we go. To count higher we add another column and start again so ordinary 16 is represented by "10" (that's "one-zero" HEX) and we count onwards in HEX ....
10 11 12 13 14 15 16 17 18 19 1A 1B 1C 1D 1E 1F
..and if you've followed so far you will understand that "1F" HEX represents a 16 in the first column plus a 15 in the second = 31 in decimal.
Can you see that "20" HEX must be 32 ?
Now, we can convert binary to HEX very easily:-
8 4 2 1
0 0 0 0 = 0
0 0 0 1 = 1
0 0 1 0 = 2
0 0 1 1 = 3
0 1 0 0 = 4
0 1 0 1 = 5
0 1 1 0 = 6
0 1 1 1 = 7
1 0 0 0 = 8
1 0 0 1 = 9
1 0 1 0 = A
1 0 1 1 = B
1 1 0 0 = C
1 1 0 1 = D
1 1 1 0 = E
1 1 1 1 = F
You seldom need to consider decimal numbers at all. Usually you can go directly from binary to hex.
Get used to splitting the binary number into groups of four, with the Least Significant Bit (LSB) on the right hand side. If you split it up, then - it doesn't matter how big it is - you can always convert each group into hex and achieve the complete answer. Consider the following 11 Bit number:-
1024 512 256 128 64 32 16 8 4 2 1
0 1 0 0 0 1 1 1 0 1 1
can be written as
8 4 2 1 8 4 2 1 8 4 2 1
0 1 0 0 0 1 1 1 0 1 1
= 2 + 2 +1 + 8 + 2 +1
= 2 3 B
= 23B HEX
Since this was an 11 Bit number it could not be divided exactly into groups of four but, as you see, it didn't matter. We ignore any bits missing at the left hand side, as if they were zero.
If we always split the binary codes into groups of four, the conversion remains easy:-
8 4 2 1 8 4 2 1 8 4 2 1 1 0 0 1 1 1 1 1 0 0 0 0 = 9 F 0
1 1 1 0 1 0 1 0 1 0 0 1 = E A 9
0 0 0 1 0 1 0 1 0 0 1 = A 9
If you can count up to sixteen you can use Hexadecimal!
Microprocessors A microprocessor often uses an Eprom to store information on a permanent basis. This sort of information is put in by the equipment manufacturer and remains unchanged. The microprocessor can read it but can not change it. The Eprom is truly a Read Only Memory. To gain access to a piece of information, the microprocessor simply pulls the Eprom input pins high or low to make the appropriate binary address then reads the contents of that address location on the Eprom eight output pins. The microprocessor then changes the address code to read information from another location. It can do this extremely rapidly. The Eprom may contain the actual program code which the microprocessor is using to tell it what to do. Alternatively, the Eprom may simply be acting as a look-up table for a set of values. A good example of this latter use is in an automobile engine management system where the engine parameters are monitored by sensors and used to generate an address code which contains the information about the quantity of air, fuel and ignition timing to use. The parameters (temperature, RPM etc.) are changing continually so the address code is also changing. | 
